대학교 시절에 내 머리를 꽝! 때린 기막힌 이론이 있었다. 지금 내 기억으론 영상처리개론 이였던가? 자료구조 시간이였던가?
하여튼 무슨 압축방식에 대한 알고리즘을 배우고 있던 시간이였는데.. 아~! 영상처리개론 이였던거같다. 어찌됐던 간에 그당시 한참 열공중이던 나에게 더욱 불을 짚혔던 이론인데... 그 이론의 정확한 이름이 기억이 안나 네이버에서 검색을 해볼수가 없었다. 그러던중 책을 보다가 이 이론에 대한 글이 있어 나중에 또 까먹을까 아예 블로그에 포스팅한다. (난 내 자신의 머리를 믿지 않는다. 오늘 본 글도 내일이면 잊어버리기 때문에 어딘가에 정리해둘 필요가 있다.) 글을 길게 쓰는건 정말 싫어한다. 그러나 기승전결이있듯이, 워밍업을 위해 한번 옛기억을 끄적여봤다.
자 본론으로 들어가자, 그렇다 내가 말하고싶은 이론은
허프만 코딩
이다.
그렇다 허프만(D. A. Huffman)은 사람이름이다.
전산 계열 전공으로 졸업한 사람은 아마도 잘알고 있을 것이다. 정확히 내가 대학시절에 배운 이론은
허프만 트리
법칙이다. 이 이론의 핵심은 간단한데..
"반복해서 사용되는 데이터는 8비트보다 적은 비트 수로 나타내지만, 별로 사용되지 않는 데이터를 나타낼 때는 8비트 이상을 사용해도 상관 없다"
요거다. 요게 다야 진짜라니깐. ;ㅡ.- 식은땀이... 지갱(대학시절부터 있었던 별명) 요런거 가지고 감동했었어?? 라고 말할지도 모르겠다만...
그 당시 안돌아가는 머리를 둘려가며 공부하던 시절 허프만 이라는 외국인이 생각해낸 이 이론이 정말 신기해 보였다. 이런 발상을 해내다뉘~! 믿을수없어~!
자 이제 가장 중요한 부분이다. 위의 문장을 해석 해보자
반복해서 사용되는 데이터
반복해서 사용되는 데이터를 뽑아내자 그래 이것까지는 그다지 어렵지 않다. 한 바이트(byte)씩 비교하면서 각각 character(C는 char가 1byte다.)에 맞게 카운터를 세서 정렬하면 될것이다.
반복 사용되는 데이터는 8비트 보다 적은 비트 수로 나타내지만,
여기서 부터가 문제다.
어떤식으로 풀어가야 할까? 흠.. 여기서 한가지 전산계열이 아닌 사람들을 위해서 데이터가 어떤식으로 들어가는지에 대해 부가 설명이 필요 할꺼같다.
우리가 메모장에 글을 쓴다고 치자 'A'라는 글씨를 치고 저장하면 그 파일은 1byte파일이 된다.( 사실 실제로 속성들어가서 보면 1byte를 훨씬넘을 것이다. 그 이유는 하드디스크의 물리적 저장방식때문으로...하나의 섹터와 .....클러스터. 주절주절..여기서 그게 요점은 아니니 나중에 HDD에 대해 글을 쓸 기회가 있으면 거기서...) 엊제든 이론상으론 1byte가 저장되어있는 것이다.~!
헌데 여기서 그치 영문은 1byte 한글은 2byte 이것까지는 알아야 다음으로 이야기가 넘어갈 수 있다.
약간의 수학인데
1byte = 8bit, 8bit = 2^8(2의 8승), 2^8 = 256
한마디로 1byte 가 8bit라는 소리다. 8bit는 00000000 이렇게 2진수 8자리라는 뜻이고, 이 2진수 8자리로 한 문자를 완성시키는 것이다.
반복사용 되는 문자를 8비트 보다 적은 최적의 비트 수로 나타내는 것이 관건인데...
눈으로 직접보는것이 백번설명보다 이해가 빠르겠지
"AAAAABBCDDEEEEEF"
문자열이 있다. 이것을 압축하지 않은 쌩날 데이터로 표현하자면
(밑에 알파벳이 이런식으로 저장된다고 가정하자 사실 이렇게 들어가진 않는데.. 편의상)
A: 00000001
B: 00000010
C: 00000100
D: 00001000
E: 00010000
F: 00100000
.
.
.
8자리로 끈어서 읽어보면 위 데이터와 같다."0000000100000001000000010000000100000001000000010000001000000010000001000000100000001000000100000001000000010000000100000001000000100000"
위처럼 17문자 * 8bit = 136bit를 사용 중인 것이다.
그런데 많이 사용되는 데이터 순으로 카운트를 해서 8bit보다 적은 bit로 표현해 저장을 한다면
A: 6번 : 0
E: 5번 : 1
B: 2번 : 10
D: 2번 : 11
C: 1번 : 100
F: 1번 : 101
이렇게 표현 될수 있는데.. 이대로 데이터를 저장해보겠다.
"00000010101001111111111101"
저장은 됐지만 복구는?
위 데이터를 복구 한다고 해보자 "00000010101001111111111101" 앞에서 부터 차근차근 읽어가면서 어떤 글씨를 저장한 것인지를 풀어갈 것 이다."AAAAABBCDDEEEEEF" 값을 모른다고 했을때 위의 코드에서 어디서 어디까지 비트가 무슨 글씨를 나타내는것인지를 알 수 있는 방법이 없다. 물론 초반에 시작하는 "0000..."은 A라는 문자라는 것을 유추할 수 없지만 '1'이 나오는 비트 부터는 어디서 부터 어디까지 문자를 표현하는 것인지 유추하기 힘들다.
이제 진짜 본론이다. 위의 문제점을 해결하기 위한 계산 방법이
허프만 트리
이다.
흠.. 이것은 트리니까 그림으로 표현을 해야하는데..
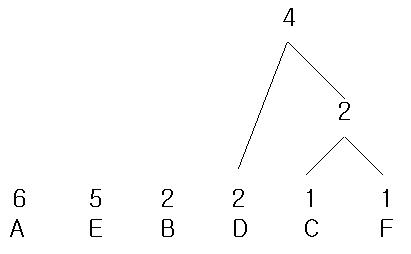
그리고 다시 정렬.
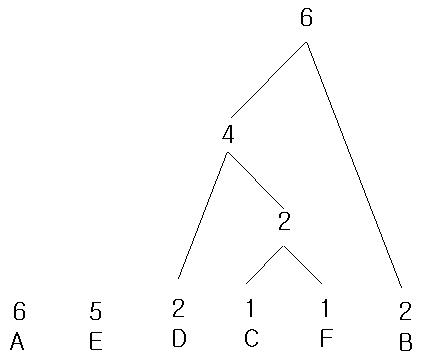
여기까지 왔으면 대충 감이 오지?? 그렇다?! 정렬후 제일 오른쪽 값과 근접한 왼쪽 값과 계속 더해주는거다.
다음 그림도 대충 감이 올것이다.
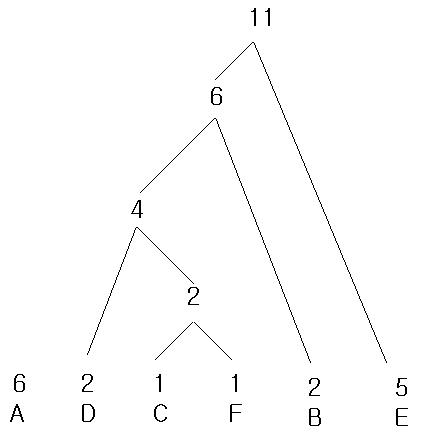
간단하다. 처음 이해 하기가 어려워서 그렇지 계속 하다 보면 아항~! 하고 자신도 모르게 왼쪽 무릅을 왼손으로 탁! 칠것이다.!!
이제 마지막 완성된 트리 구조다.
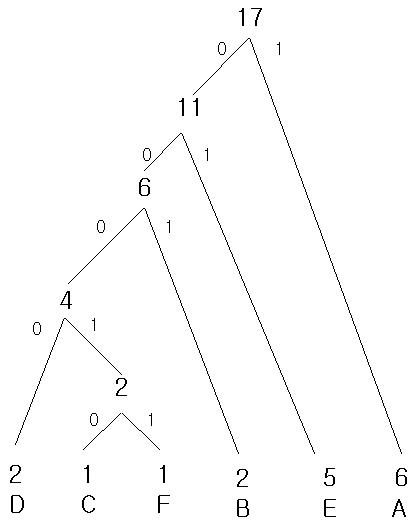
이렇게 해서 얻은 bit값은
A: 1
E: 01
B: 001
D: 0000
C: 00010
F: 00011
.
.
물론 실데이터를 처리 했을 경우엔 이보다 더 많은 문자열이 나오므로 8bit를 넘기는 문자도 있겠지만 그것또한 최소한의 반복문자이기 때문에 상관하지 않는다.
엊제든 이렇게 해서 압축이 이루어졌다. 이것을 2진수로 표현해보면 ("AAAAAABBCDDEEEEEF" 였다.)
"1111110010010001000000000010101010100011"
"1 1 1 1 1 1 001 001 00010 0000 0000 01 01 01 01 01 00011"
이렇게 된다. 물론 이 데이터 말고도 각 문자가 어떤 비트값을 가지고있는지에 대한 정보도 같이 넣어서 파일에 기록해둔다.
이렇게 압축이 끝이났다. 그럼 데이터를 복구 시킬때 어떻게 하느냐~?! 라고 의문을 가지시는 분들도 있겠는데.. 위의 허프만 부호 정보를 가지고 앞에서 부터 차례대로 해석해 보면 금방 이해가 갈것이다.
이 글을 쓰게 된 이유는 나의 건망증을 위해서인 것도 있지만 이런 이론도 있다는 것을 소개해 주고싶었으며(사실 이 이론은 모르는 사람도 꽤된다. 네이버에도 자세히 설명되어있는 블로그를 찾기 힘들어 내가 직접쓴것이다.) 좀더 폭넓은 생각으로 문제 해결능력을 키워 나갔으면 하는 마음에서 글을 쓴다.휴~ 길었다. 프리젠테이션 -> 그림판 신공으로 그림까지 오늘 많이 무리했다.
'algorithm' 카테고리의 다른 글
| 정렬알고리즘(Sort algorithm source) (1) | 2008.02.18 |
|---|---|
| 자료구조 - 스택(Stack) (1) | 2007.12.17 |
| 자료구조 - 연결 리스트 (Linked List) (0) | 2007.12.17 |
| 자료구조의 종류 (0) | 2007.12.17 |
| 자료구조의 구성 (0) | 2007.12.17 |